

博士!
「へいほうかんせい」ってどうやったらいいの?

平方完成じゃな。
これはいくつか覚えておくことがあってな。
それを覚えていないと理解できずに躓いてしまうんじゃが、それほど難しくはないぞい。

そうなの?
周りの子も「全くわからん」って言ってたから、てっきりすごく難しいのかと思ってたよ。

順番に覚える必要があって、途中を飛ばすと途端に理解できなくなるからの。
落ち着いてやれば問題ないのじゃ。
平方完成をやるまでに覚えておくこと
平方は2乗
平方(へいほう)とは、「2乗(に じょう)」のことです。
\(m^2\)(平方メートル)という単位を使ったことがあると思いますが、それに出てくる平方と同じことです。
平方完成(平方を完成させる)とは、\((x-1)^2\)など平方の形(2乗の形)に書き換えることをいいます。

平方完成をしているのに、2乗をつけ忘れることが多いのじゃ。
()の展開ができる
\(2(a-2)=2a-4\)
上のように、()の展開ができるようになっておきましょう。
\((x+1)^2=x^2+2x+1\)
2乗のときの展開もできるようになりましょう。

\((x+a)^2=x^2+2ax+a^2\) の展開を理解せずに平方完成をしようとする人が驚くほど多いのじゃ。
共通因数を取り出せる
\(2x-4=2(x-2)\)
上のように、共通する因数を()の外に取り出すことができるようになっておきましょう。
\(3x-5=3(x-\frac{5}{3})\)
上ができるようになると、平方完成は問題なくできます。

共通因数を取り出す必要があるところで躓くことが多いのじゃ。

5の中に3なんてないけど…。

展開して元に戻せるなら問題無しじゃ。
因数分解と平方完成の違いの把握
平方完成に入っていく前にこちらの展開をしてみましょう。
\((x+1)^2=x^2+2x+1\)
2乗の式を展開して、2次関数の式になりました。では、この式を逆にしてみましょう。
\(x^2+2x+1=(x+1)^2\)
2次関数から2乗の式に書き換わりました。これを因数分解という言い方をしていましたが、ここでは平方完成という言い方もしてます。この場合は同じことですが、平方完成は因数分解と少し違います。
次を見てみましょう。
\((x+1)^2+1=x^2+2x+2\)
\(x^2+2x+2=(x+1)^2+1\)
因数分解は( )だけの式にするのですが、平方完成は、「\(( )^2\)+数字」の形に直すことを言います。
ここが因数分解と平方完成の違うところで、少し難しげな感じがしてしまう原因でもあります。
平方完成のやり方
問1:\(x^2+2x\)
\(x^2+2x\)
これを平方完成してみましょう。「\(( )^2\) +数字」の形に変形するのが平方完成です。
では、( )の中身はなんでしょう。
\(( )^2\) を展開したときに、\(x^2+2x\) が出てくるようなものを考えればいいですね。

そんなの無理難題だよ。
パッと見、難しいですよね。でもやり方を知っていれば難しくありません。展開の公式を見てみましょう。
\((x+a)^2=x^2+2ax+a^2\)
この「\(x^2+2ax\)」に注目です。
「\(a\)」にどんな数字が入れば、「\(x^2+2ax\)」が「\(x^2+2x\)」になるかを考えましょう。

「1」だね。
つまり、「\((x+1)^2\) 」を展開すれば、「\(x^2+2x\)」が出てくると予想できます。実際に、展開してみましょう。
\((x+1)^2=x^2+2x+1\)
展開ができましたが、右側に最初の式と違うところがありますね。わかりますか?

最初の式「\(x^2+2x\)」になかった数字が増えてるね。
そうです。右側の「+1」というのは最初の式にありませんでした。
平方完成は「=(イコール)」で式を繋ぐので、辻褄をあわせる必要があります。どうすればいいのかわかりますか?

「+1」がいらないので「-1」をすれば「0」になって消えるんじゃない?
その通り。したがって、次の式の形になります。(両辺を「-1」します。)
\((x+1)^2-1=x^2+2x+1-1\)
計算できるところは計算しましょう。
\((x+1)^2-1=x^2+2x\)
あとは左右をひっくり返しましょう。
\(x^2+2x=(x+1)^2-1\)
これで平方完成ができました。

なんとなくわかったけど、手順が多くてわかりにくいよ。
まとめていきます。
\(x^2+2x\)
\(( )^2\) は展開したときに\(x\)の係数(\(x\)の前にある数字)は必ず2倍されているので、出ている数字を半分にすれば元に戻せることがわかります。
つまり、\(2x\) の「2」というのは2倍されているので、半分の「1」が展開前の数です。
したがって、\((x+1)^2\) です。
このままでは「=」ではないので、「-1」をして「\((x+1)^2-1\)」にしましょう。
\(x^2+2x=(x+1)^2-1\)
平方完成はこれで終了ですが、もう一歩理解を深めます。
式の右側(右辺)を展開して計算すると、式の左側(左辺)の式に戻ることを確認しましょう。
\begin{eqnarray} (x+1)^2-1 &=& x^2+2x+1-1\\ &=& x^2+2x\end{eqnarray}
どうして「-1」をする必要があったのかがわかると思います。

展開すると元の式に戻るというのが重要じゃ。
戻らなければ「=」ではないのだよ。
問2:\(x^2+2ax\)
\(x^2+2ax\)
もう少し理解を深めるために、「\(x^2+2ax\)」を平方完成してみましょう。
「\(x\)」の係数「\(2a\)」の半分である「\(a\)」が出てくるのでしたね。
\(x^2+2ax=(x+a)^2-a^2\)
先程「-1」していたのは、半分して出てきた数「\(a\)」を2乗したものというのがわかります。
つまり手順はこんな感じです。
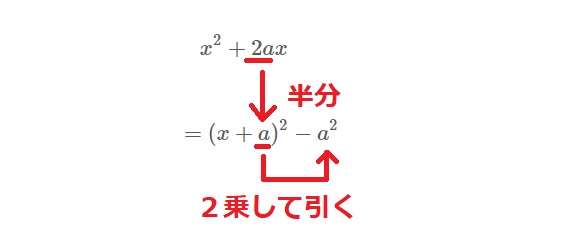
- 「\(x\)」の係数を半分にする
- 「\((x+○)^2\)」の○の部分に半分にした数字を代入
- 代入した数字を2乗して引く
どうして代入した数字を2乗して引く必要があるのかについては、( )を展開してみるとわかると思います。

展開して元に戻ることを確認する癖をつけておくと理解が早いぞい。
問3:\(x^2+2x+3\)
\(x^2+2x+3\)
次はこちらを平方完成してみましょう。
見る部分は「\(x^2+2x\)」で、「+3」の部分は置いておきます。
「\(x^2+2x\)」の平方完成は、問1で最初にやりましたので省略します。覚えていない人は戻って確認してみてください。
\begin{eqnarray} x^2+2x+3 &=& (x+1)^2-1^2+3 \\ &=& (x+1)^2-1+3 \\ &=& (x+1)^2+2 \end{eqnarray}
「\(x^2+2x\)」の平方完成をしたあと、置いておいた「+3」を付け足すだけですね。

この問題がわからないという人は、問1や2で数字を変えて試してみるのじゃ。展開して元に戻すことも大事じゃぞ。
問4:\(2x^2+4x\)
\(2x^2+4x\)
「\(x^2\)」の前に係数があると、途端に難しくなります。まずは簡単なものから平方完成してみることにしましょう。
平方完成するときは「\(x^2\)」に係数があるとできません。したがって、係数を外に出す必要があります。
\(2x^2+4x=2(x^2+2x)\)
ここまで準備できれば平方完成していけます。「\(x^2+2x\)」の平方完成は問1でやったので省略します。
\begin{eqnarray} 2x^2+4x &=& 2(x^2+2x) \\ &=& 2\left\{(x+1)^2-1 \right\}\end{eqnarray}
なぜ{ }(中カッコ)がついているかというと、この前についている2というのは「\(x^2+2x\)」全体を2倍しているため、中身だけ変形しても全体の2倍は消えないからです。そのことを忘れないように{ }がついています。

忘れないからといって{ }を書かなくていいわけではないので注意するのじゃ。
{ }が入った状態では平方完成ができているとは言えないので、展開する必要があります。
\begin{eqnarray} 2x^2+4x &=& 2(x^2+2x) \\ &=& 2\left\{(x+1)^2-1 \right\}\\ &=& 2(x+1)^2-2\end{eqnarray}
これで終了です。

{ }の展開は「\(2(x-1)=2x-2\)」と同じように展開したらいいんだね。

その通りじゃ。
問5:\(2x^2+4x+3\)
\(2x^2+4x+3\)
「\(x^2\)」の前に係数があるだけなく、「+3」もついています。やることは、問3と同じです。
\begin{eqnarray} 2x^2+4x+3 &=& 2(x^2+2x)+3 \\ &=& 2\left\{(x+1)^2-1 \right\}+3\\ &=& 2(x+1)^2-2+3 \\ &=& 2(x+1)^2+1 \end{eqnarray}

だんだん難しくなってくるね。

順番に覚えていけば大丈夫じゃ。
問6:\(x^2+3x\)
\(x^2+3x\)
これまでのことがわかっていれば、恐れることはないです。半分にして2乗したものを引くのです。
\begin{eqnarray} x^2+3x &=& (x+\frac{3}{2})^2-(\frac{3}{2})^2 \\ &=& (x+\frac{3}{2})^2-\frac{3^2}{2^2}\\ &=& (x+\frac{3}{2})^2-\frac{9}{4} \end{eqnarray}

3の半分は、1.5じゃが、1.5を2乗するのは計算が大変じゃ。
\(\frac{3}{2}\)にしたほうが計算が楽じゃの。
問7:\(x^2+3x+3\)
\(x^2+3x+3\)
「+3」をつけて平方完成をしてみましょう。
\begin{eqnarray} x^2+3x+3 &=& (x+\frac{3}{2})^2-(\frac{3}{2})^2+3 \\ &=& (x+\frac{3}{2})^2-\frac{3^2}{2^2}+3\\ &=& (x+\frac{3}{2})^2-\frac{9}{4}+ \frac{12}{4}\\ &=& (x+\frac{3}{2})^2+\frac{3}{4}\end{eqnarray}

分数は通分して計算するんだね。
問8:\(2x^2+3x+3\)
\(2x^2+3x+3\)
では、最後にこれを平方完成してみましょう。今までの集大成です。
\begin{eqnarray} 2x^2+3x+3 &=& 2(x^2+\frac{3}{2}x)+3 \\ &=& 2\left\{(x+\frac{3}{4})^2-(\frac{3}{4})^2 \right\}+3 \\ &=& 2\left\{(x+\frac{3}{4})^2-\frac{3^2}{4^2} \right\}+3 \\ &=& 2\left\{(x+\frac{3}{4})^2-\frac{9}{16} \right\}+3 \\ &=& 2(x+\frac{3}{4})^2-\frac{9}{8}+3 \\ &=& 2(x+\frac{3}{4})^2-\frac{9}{8}+\frac{24}{8} \\ &=& 2(x+\frac{3}{4})^2+\frac{15}{8}\end{eqnarray}
あとがき
これで平方完成はできるようになったかと思います。
問を順番に進めていき、わからなくなったところで、問を戻ったり、展開して元の式に戻したりしながら問題に慣れていきましょう。
もし初めからわからないときは、やるまでに覚えておくことができるようになってから再挑戦したらいいと思います。




コメント