

博士!
組合せでCの計算のやり方がいまいち納得いかないんだけど。

ふむ。
どこが納得行かないんじゃ?

順列を順列で割ると組合せになる意味がよくわからないとこ。

なるほど。
割り算の仕組みから復習する必要があるようじゃ。

そんなところから復習が必要なの!?

ゆっくり、見ていこうかの。
割り算には2つの考え方がある
「24÷6」を考えてみましょう。
- 24の中に6がいくつ入っているか。(答え、4つ)
- 24を6等分した1つ分はいくつか。(答え、4つ)
図にするとこのようになります。
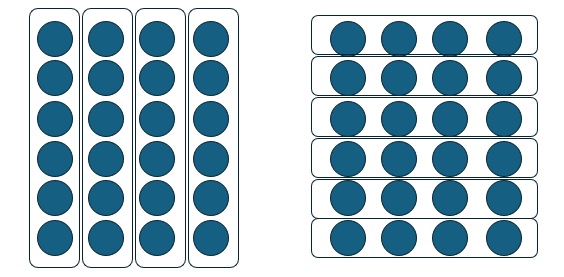
答えはどちらも「4」になるのですが、図が違いますよね。
これの区別がついていないと、割り算をうまく使うことができないので、しっかりと考えるようにしましょう。
時速の計算など、割合で躓いている人はこの区別がついていない人が多いです。

組合せで使う方は、どちらか考えてみるのじゃ。
組合せを学ぶ手順
順列の求め方を理解しよう
組合せに入って行く前に順列の復習からしていきましょう。
この問いを考えます。
このとき、4つの文字を並べるため、四角を4つ書きます。
□□□□
一番左から順番に文字を入れていきます。
- 一番左:a,b,c,dから1つを選ぶので、選び方は4通り
- 左から2つ目:一番左で選んだ文字以外の3つから1つを選ぶので、選び方は3通り
- 左から3つ目:残り2つの文字から1つ選ぶので、選び方は2通り
- 一番右:残り1つなので、選び方は1通り
したがって、4✕3✕2✕1を計算すればいいので、答えは「24通り」です。
順列のPや!(階乗)を使うと以下のような式になります。
\(4!={}_4\mathrm{P}_4=4\times3\times2\times1=24\)

一番左に「a」を入れると、
その次は「b,c,d」の3つから1つ選ぶってことだね。

選べる文字が1つずつ減って行くのじゃ。
もう一問考えてみましょう。
先程と同じように考えます。3つの文字を並べるため、四角を3つ書きます。
□□□
一番左から順番に文字を入れていきます。
- 一番左:a,b,c,dから1つを選ぶので、選び方は4通り
- 左から2つ目:一番左で選んだ文字以外の3つから1つを選ぶので、選び方は3通り
- 一番右:残り2つの文字から1つ選ぶので、選び方は2通り
したがって、4✕3✕2を計算すればいいので、答えは「24通り」です。
順列のPを使うと以下のような式になります。
\({}_4\mathrm{P}_3=4\times3\times2=24\)

4つから3つ選んで並べるから、
\({}_4\mathrm{P}_3\)なんだね。

その通りじゃ。
順列は大丈夫そうじゃの。
順列と組合せの違いを理解しよう。
順列と組合せの違いは、言葉で書くと簡単です。
- 順列:選んで並べる
- 組合せ:選んで並べない(選ぶだけ)
では、選ぶというのはどういうことでしょうか。
a,b,c,dの4つから3つ選んでみます。「a,b,c」を選びました。ここまでは大丈夫ですね。選んだだけです。
ここから、並べるときと、並べないときを見てみましょう。
- (順列)並べる:abc,acb,bac,bca,cab,cba(6通り)
- (組合せ)並べない:abc(1通り)
並べるとそれぞれ数える必要があるのですが、並べなければそのまま数えなくていいですね。
見た目では、選んで並べない組合せの方が簡単に見えるのですが、それをそのまま計算で出そうとしても出せません。組合せは、順列を一度求めてからグループごとにまとめる必要があるので難しく見えてしまい、苦手に思ってしまうことが多いです。

計算ではいきなり答えを出せないんだね。

一度並べてからグループごとにまとめる必要があるのじゃ。

グループごとにまとめるってどういうこと?

割り算を使うのじゃ。
組合せはグループ分けと同じ
次の問いを考えてみましょう。
まずは、a,b,c,dから3つ選んで並べてみましょう。さきほどやりましたね。
\({}_4\mathrm{P}_3=4\times3\times2=24\)
この24の中にある同じ文字の組合せを1つのグループでまとめます。(同じメンバーは同じグループでまとめてしまうということです。)
- (順列)並べる:abc,acb,bac,bca,cab,cba(6通り)
- (組合せ)並べない:abc(1通り)
6通りを1通りにまとめることができますね。
さて、この並べて数えた6通りを計算で出せるようになりましょう。3つすべてを1列に並べるのと同じです。
\(3!={}_3\mathrm{P}_3=3\times2\times1=6\)
どのグループも、この6通りの並べ方があるというのはわかりますね。

1つのグループだけ、5通りになったりしないってことだね。
あとは、24の中にこの6通りのグループがいくつ入っているのかがわかれば答えが出ますね。
ここで最初に確認した割り算を使いましょう。24の中に6がいくつ入っているかは、「24÷6」でしたね。
したがって、答えは「4」です。
ここまでを式でまとめてみると以下のようになります。
\({}_4\mathrm{ C }_3=\frac{{}_4\mathrm{P}_3}{3!}=\frac{4\times3\times2}{3\times2\times1}=4\)

なぜ割り算を使うのかがわかったかな。

1つのグループに入っている数が同じだから、
割り算を使って求められるんだね。
練習問題
クリック(タップ)で答えが出ます。
\begin{eqnarray} {}_5\mathrm{ C }_3 &=& \frac{{}_5\mathrm{P}_3}{3!} \\ &=& \frac{5\times4\times3}{3\times2\times1} \\ &=& 10 \end{eqnarray}
答え、10通り
\begin{eqnarray} {}_6\mathrm{ C }_2\times{}_4\mathrm{ C }_2\times{}_2\mathrm{ C }_2 &=& \frac{6\times5}{2\times1}\times\frac{4\times3}{2\times1}\times\frac{2\times1}{2\times1} \\ &=& 90 \end{eqnarray}
答え、90通り
問2でA,B,Cと分けていたのがなくなる。
つまり、「ABC,ACB,BAC,BCA,CAB,CBA」が1つのグループでまとまるので、「90÷6=15」
詳しく書くと以下の式になる。
\begin{eqnarray} {}_6\mathrm{ C }_2\times{}_4\mathrm{ C }_2\times{}_2\mathrm{ C }_2\times\frac{1}{3!} &=& \frac{6\times5}{2\times1}\times\frac{4\times3}{2\times1}\times\frac{2\times1}{2\times1}\times\frac{1}{3\times2\times1} \\ &=& 15 \end{eqnarray}
答え、15通り

1つのグループでまとめるときは割り算
1つのグループでまとめるときは割り算
1つのグループでまとめるときは割り算
1つのグループでまとめるときは割り算

組合せの難しい問題は、
どう割るかをよく考えるといいのじゃ。
あとがき
問題に慣れるために、いくつか自分で問題を解いてみるようにしましょう。
また、割り算をするときは、「いくつ分」「等分」のどちらの意味で使っているのかよく考えるようにしましょう。
そうすれば、組合せのところ以外の統計などで、\(Z=\frac{X-m}{\sigma}\)という式がいきなり出てきても、\(X-m\)が\(\sigma\)のいくつ分なのかが知りたいし、それがわかれば解けるということがわかるようになります。





コメント