

博士!
因数分解について教えて!

高校になってもつまづいている生徒が多いところじゃな。
まずはイメージで覚えるのが大事じゃ。

イメージ?
やり方じゃなくて?

因数分解と聞いてイメージできるようにならないと、いつまで経っても覚えられないからじゃ。

「因数分解?ああ、これのこと?」
ってわかるようになればいいのかな。

その通りじゃ。
まずはイメージをつかもう
カレーで覚えよう
例えば、カレーを作ろうと思って材料を用意するとします。何を準備しますか?
- カレーのルー
- じゃがいも
- にんじん
- たまねぎ
- にく
- 水
これらを料理するとカレーになるわけですが、それを式で書くとこんな感じになります。
カレー=(カレーのルー)×(じゃがいも)×(にんじん)×(たまねぎ)×(肉)×(水)
カレーというのがそれぞれの材料の形で見えるようになりました。この材料が因数と呼ばれていてで、完成品を元の材料の形に分解するので因数分解といいます。
つまり、因数分解は元になっている材料がいったい何なのかということを聞いているわけですね。
長方形の面積で覚えよう
長方形の面積の求め方は、「たて×よこ」ですよね。
例えば、10の面積であれば以下のような計算の仕方が考えられます。
- 1×10
- 2×5
- 5×2
- 10×1
こんなふうに、「たて」と「よこ」の数字で面積ができているわけですね。
先程のカレーの例と同じように考えると、「たて」「よこ」が面積の材料(因数)というわけです。
つまり、因数分解というのは、数字を長方形だと思って、「たて」「よこ」の数字を求めているわけです。

全ての数字は長方形と思っていたらいいんだね。

そうじゃ。
因数分解ってどうして難しいの?
因数分解が難しいなと思う理由ですが、多項式が長方形に全く見えないからです。
例えば、「10」であれば、「2×5」とすぐに出せますが、「\(x^2+7x+12\)」と書かれると、「あれ?これって長方形?」となるわけですね。
これをどうやって長方形の面積の形にイメージするのか、というところでつまづいてしまうわけです。

どう頑張ってみても長方形には見えないね。

複数の長方形の組み合わせになるからの。
ぱっと見ではわからんよ。
例えば、63というのを因数分解してみましょう。
「7×9=63」なので、「7」「9」が出てきますね。
この「7」と「9」を更にわけて、「7=4+3」「9=5+4」という形に直してみるとどうなるでしょうか。
つまり、(4+3)×(5+4)というわけです。長方形の図にすると以下の通りになります。
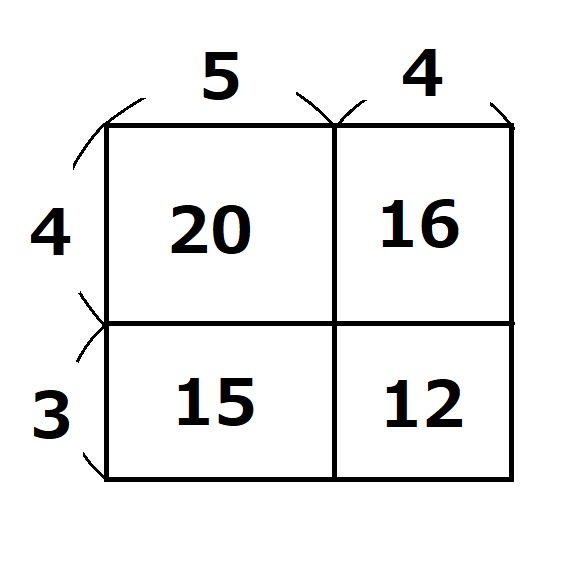
63からこの図をいきなり考えろと言われても無理ですね。

こりゃ、思いつかん。
そこで、因数分解の問題には毎回ヒントと簡単になるルールがあります。
因数分解の3つのルールを理解しよう
同じ数字が出てくる
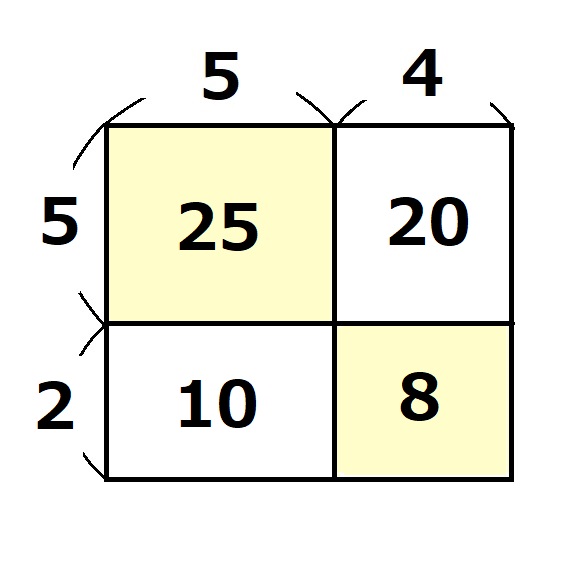
因数分解のルールですが、左上の面積を求める「たて」「よこ」に同じ数字を配置します。
同じ数字になるので、面積はその数字の2乗になります。ここでは「5×5=25」ですね。
残りの数字のかけ算

右下は、先程使った同じ数字以外の数字のかけ算になります。
ここでは、「2×4=8」ですね。
残りの面積は、たし算する
残った左下の「10(2×5)」と右上の「20(5×4)」は、たし算します。「10+20=30」ですね。
これで文字の入った因数分解を解くための準備が終わりました。ここまでのことをまとめます。
「63」という数字は、「25」「8」「30」に分けることができ、この手順を追っていくことで因数分解が可能です。
実際に因数分解してみよう
\(x^2+7x+12\)を因数分解することにします。
\(x^2\)と\(7x\)と\(12\)に分かれているのでこれを使っていきます。
やることは3つでしたね。
- 同じ数の2乗
- 残りの数のかけ算
- 残りの面積のたし算
同じ数の2乗
文字を使った因数分解では、同じ数の2乗の部分が必ず文字になります。つまり以下のとおりです。
- 同じ数の2乗(\(x^2\))
- 残りの数のかけ算
- 残りの面積のたし算
残りは\(7x\)と\(12\)の2つですね。
残りの数のかけ算
(使った文字は使わない)残りの数字のかけ算なので文字の入っていない\(12\)を使います。
かけ算の順番は気にしなくてもいいので考えられるのは以下のとおりです。
- 1×12
- 2×6
- 3×4
この3つの中から残りの組み合わせを考えます。
残りの面積のたし算
さきほど求めた数字の組み合わせで、文字をかけたものが面積です。
つまり、「1と12」「2と6」「3と4」の中で、足して7になる組み合わせを探します。
3と4ですね。
これで準備完了です。あとは、これまででわかった数字をまとめていきます。
長方形に直して考える
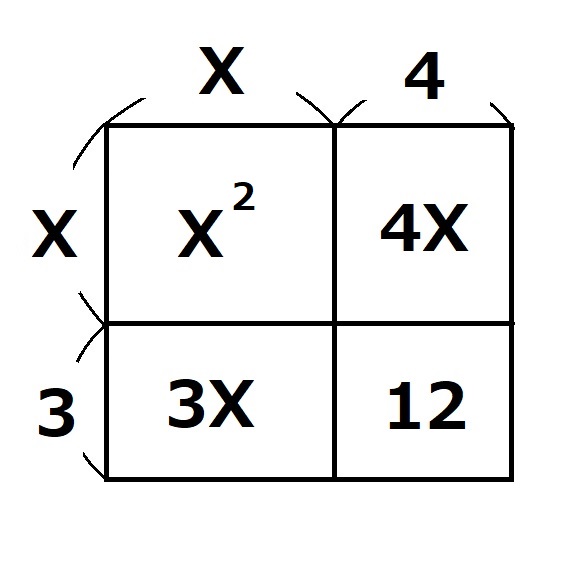
今までやったことを図にしてみるとこうなります。
- 同じ数の2乗(\(x^2\))
- 残りの数のかけ算(\(12=3×4\))
- 残りの面積のたし算(\(7x\))
結局、因数分解するためにやったことは、(\(12=3×4\))の部分です。
この「3」「4」を使えば、残りの面積「\(3x\)」「\(4x\)」が出せるわけですね。
したがって、\(x^2+7x+12=(x+3)(x+4)\)が答えです。
因数分解ができないと嘆く人は、この残りの面積部分がちんぷんかんぷんになってしまってます。落ち着いて考えれば大丈夫なのでわからない人は深呼吸をして最初から読み直しましょう。
式のまま考える
ここまでのことを理解するともっと簡単にまとめられます。
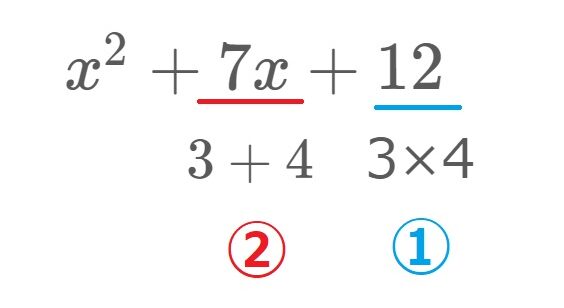
- \(12=□×△\)になる□と△を予想する
- \((□+△)x=7x\)になる□と△を確定する
これで□と△に「3」と「4」が入るので、\(x^2+7x+12=(x+3)(x+4)\)が答えです。

かけて12、たして7になる数な~んだ?
3と4だね。
あとがき
これで基本的な因数分解が求められるようになります。
これをうまく使うことで、3次関数や三角関数の因数分解もできるようになるので、しっかり覚えておきましょう。
これをマスターしてから、「たすき掛け」を使用する \(ax^2+bx+c\) の因数分解に入っていきましょう。学校の授業ではマスターする暇もなく次に進んでいくと思います。そういうときは、授業で勉強するのではなく休み時間や放課後、家で勉強すればいいんです。

授業以外で勉強するのってズルくない?

自学自習は反則技だと思っている人が多いんじゃが、反則ではないからの。
ズルくないから、落ち着いて勉強するんじゃ。




コメント