

博士!
時速の計算を「みはじ」で覚えたんだけど、もっと簡単な方法はないの?

「みはじ」「きはじ」「はじき」の法則というやつじゃな。
これはけっこう難しいんじゃぞ。普通に計算したほうがよほど簡単じゃ。

そうなの?
じゃあ、そのやり方を教えてよ。

では「みはじ」のやり方で考えつつ、通常の計算方法を説明していくのじゃ。
「みはじ」「きはじ」「はじき」の法則について
「みはじ」とは?
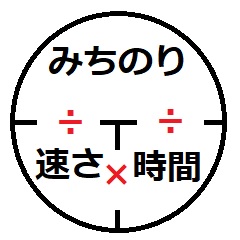
「みはじ」「きはじ」「はじき」を簡単に説明すると、上の図のことです。
- 「道のり」の「み」(距離の「き」)
- 「速さ」の「は」
- 「時間」の「じ」
それぞれの頭文字をとって「みはじ」といいます。

頭文字(かしらもじ)は、その言葉の一番初めの文字のことじゃ。
使い方ですが、求めたいものを指で隠して、余っている部分が使用する計算になります。
- 「道のり」を出したければ「速さ×時間」
- 「速さ」を出したければ「道のり÷時間」
- 「時間」を出したければ「道のり÷速さ」
これが「みはじ」の法則です。
「みはじ」が難しい理由
「みはじ」「きはじ」「はじき」が難しい理由ですが、これは問題を解くときにしていることを考えるとわかりやすいです。

実際に問題を解いてみるのじゃ。
60kmの道のりを2時間で進んだときの時速は?
この問題を「みはじ」を使って考えるときに、まず書くのが図です。

これを書くのってけっこう時間がかかりますよね。また、図が書けてからどこにどの値が当てはまるのかを考える必要があります。手順が多すぎます。
「時速」について知っていれば、図を書くことがそのまま答えになります。手順を覚えるのや「みはじ」の図を書くよりよほど簡単です。
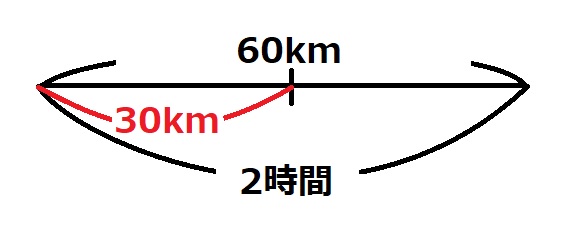
「時速」というのは、「1時間でどれだけ進むか」です。「1時間」で進む距離はパッと分かるのではないでしょうか。
2時間が1時間の2倍(2つ分)と考えることもできますし、それに合わせて、60kmの半分を考えれば答えが出るんだということも気が付きやすくなります。

問題文をそのまま図にすればいいんだね。

その通りじゃ。
「みはじ」の法則の限界
「みはじ」「きはじ」「はじき」の法則は、単位の変換に対応していません。
例えば、次の問題が出たときには計算ができなくなります。
60kmの道のりを2分で進んだときの時速は?
「みはじ」「きはじ」「はじき」の法則しか覚えていない人は、このような単位が変わる問題に対応することができません。答えに、時速30kmと書きがちです。(対応できる人は「速さ」についてわかっている人なので、「きはじ」を使わなくても解けます。)
「時速」についてわかっている人は、1時間でどれだけ進むかを考えますので、どう考えても答えが減るなんておかしいことに気が付きます。

1時間は2分の30倍(30コ分)になるので、60kmの30倍(60×30)である時速1800kmが正解になります。

求めたい値の単位が重要なんじゃ。
次で詳しく見てみるのじゃ。
時速の計算について
単位が重要
時速など「速さ」の計算で重要なのが「単位」です。
単位とは、「単位1つ分あたりいくつなのか」というのを考えるときに使います。
例えば、「10km」というのは「km」が単位なのですが、「1kmが10個分で、10kmになる」というふうに考えます。
普段こんなふうに考えたりしないと思いますが、これがとても重要になります。
時速の単位の考え方
では、時速だとどうでしょう。
「時速10km」をきちんと書くと、「10km/時間」という書き方になり、「”1時間あたり10km進む”のが何個分あるのか」というふうに考えます。
「/時間」というのが「1時間あたり」という意味で「毎時間(まいじかん)」という読み方をします。
「10km/時間」は「10キロメートルまいじかん」と読みます。1時間毎(1じかんごと)に10km進むという意味です。
時間で割ると時速になるのはなぜ?
時速の計算式は、「道のり÷時間」です。
では、「時間で割る」とはどういうことでしょうか。

どうして時間で割るんだろう?
それを考えるには、割るということがどういうことなのかを復習しましょう。
「6÷3」で考えてみます。2つの意味が考えられます。思いつきますか?
- 6の中に3がいくつ入っているのか(答え、2つ)
- 6を3等分した1つ分はいくつか(答え、2つ)
時速の場合は、この「等分」する方を考えます。(いくつ入っているのかの方は後で使います。)
60kmを2時間で割るということは、60kmを2等分しています。(30kmと30kmの2つに分かれます。)
この30km1個分は、1時間分ですよね。「1時間毎(1じかんごと)」という意味の「km/時間(キロメートルまいじかん)」という単位を使い、「30km/時間」で時速30kmが出ます。

時間で割ると1時間あたりの値が出るのじゃ。

なるほど。
このまえ社会で、人口を面積で割ったら1k㎡(1平方キロメートル)あたりの人数が出たのは、こういうことだったんだね。

その通り!
人口密度などの計算も同じじゃ。
速さで割るってどういうこと?
では最後に、速さで割るとはどういうことか問題を解いて考えてみましょう。
60kmの道のりを時速30kmで進むと何時間かかりますか?
時速というのは「1時間で進む距離」でした。これが60kmの中にいくつ分入っているのかがわかれば、合計何時間かかったかがわかりますよね。
60÷30をすると、60÷30=2なので、60の中に30が2つ分入っていることがわかり、1時間かかるのが2つ分で、答えは「2時間」です。

時間を出すのは、「いくつ分」の考え方を使うんだね。

その通りじゃ。
これで、わり算の考え方を両方使ったことになるの。
問題を解いて理解を深めよう
家からコンビニまで10km離れているとします。
- 問1:家からコンビニまで時速60kmで進むと何分で到着しますか?
- 問2:家からコンビニまで30分で到着しようと思ったら、100m何秒で走ればいいですか?

答えを見ないで、自分だけの力で問題を解いてみるのじゃ。
問1の解答
時速60kmということは、1時間で60km進むということです。
1時間=60分なので、60分で60km進むのがわかります。
ということは、10分で10km進むので、答えは10分です。
問2の解答
1km=1000mなので、10km=10000mです。
また、1分=60秒なので、30分=1800秒です。
10000mを1800秒で走ればいいので、100mは18秒になり、答えは18秒です。
あとがき
算数や数学が苦手な人は、文章を読むのが苦手なのでここに書いてあることは「ナンノコッチャ?」になると思います。
わからなくても何回も読んで、単位の考え方を身につけましょう。わからないところはコメントで聞いてくれても構いません。
これさえできるようになれば、他の単位の計算や割合、中学・高校の数学だけでなく、化学や物理の計算もつまずかずに理解できるようになります。
まずは、時速の計算で単位に慣れつつ、体積や人口密度、塩分濃度など小学生のうちに身につけておけることは身につけておきましょう。
もちろん、それ以上の年の人でも身につけて損はないです。特に、大人になると年率何%などお金のことが計算できないと大変です。なんとか身につけましょう。




コメント