

博士!
二次関数について教えて。

質問が漠然とし過ぎじゃな。
もう少し的を絞ってほしいんじゃが。

ん~全部。

仕方ない。
見ていこうかの。
二次関数の前に知っておくべき知識
関数とは?
二次関数の説明をする前に、「関数」とは何なのかについて知っておきましょう。
関数とは、ある変数\(x\)の数値が変わると、それに依存して変わる変数\(y\)のことです。このとき、「\(y\)は\(x\)の関数」といいます。
言葉だけではわかりにくいですが、1個10円のみかんを考えてみるとわかりやすいと思います。
1個が2個に変わると10円が20円に変わりますよね。この個数と値段はそれぞれ関係し合っているので、関数になりえるというわけです。式にすると「\(y=10x\)」ということですね。
お互いに関係している数字なので、関数と覚えても問題ないです。
文字の四則計算
関数の問題を解くときに必要になるのが四則(+-×÷)計算です。
- \(2a+3a=(2+3)a=5a\)
- \(2a-3a=(2-3)a=-a\)
- \(2a×3a=(2×3)×a×a=6a^2\)
- \(2a÷3a=\frac{2a}{3a}=\frac{2}{3}\)
この計算ができないと、これから習うすべてのことができなくなるので必ず習得しましょう。
一次関数グラフを書けるようになろう
\(x\)の値を決めると\(y\)の値が決まるので、いくつか値をもとめます。
\begin{array}{c|c|c|c|c|c} x & 1 & 2 & 3 & 4 & 5 \\ \hline y & 2 & 4 & 6 & 8 & 10 \\ \end{array}
この点を座標平面上に取って、あとは線を引っ張ればグラフが書けます。
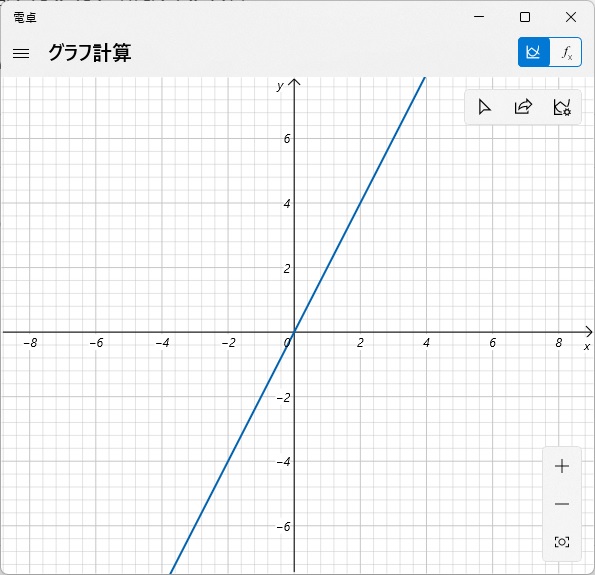
グラフの書き方は、点をいくつかとって線を引くだけです。
この点をいくつか取るというのがめんどくさくてサボりがちになるので、グラフが書けないという人が多発します。

グラフが苦手な人のほとんどは、点が取れていない。
めんどくさがらずに計算して出すのじゃ。
これから習う、二次関数、三次関数、指数関数、対数関数なども、点を計算すればすべてグラフが書けます。めんどくさがらずに計算するようにしましょう。
二次関数について
基本は何も変わらない
基本的に一次関数と何も変わりません。
グラフの書き方も点を取れば書けるし、計算のやり方もそのままです。
違いはグラフの形が固定
一次関数では、「傾き」がありました。\(y=ax\)の\(a\)ですね。
二次関数でも名前はついていませんが、一次関数の傾きのようにグラフの形を決める部分があります。
\(y=ax^2+bx+c\)の\(a\)の部分です。この部分が同じであれば、グラフの形がすべて同じ形になります。違うのは頂点の位置だけです。
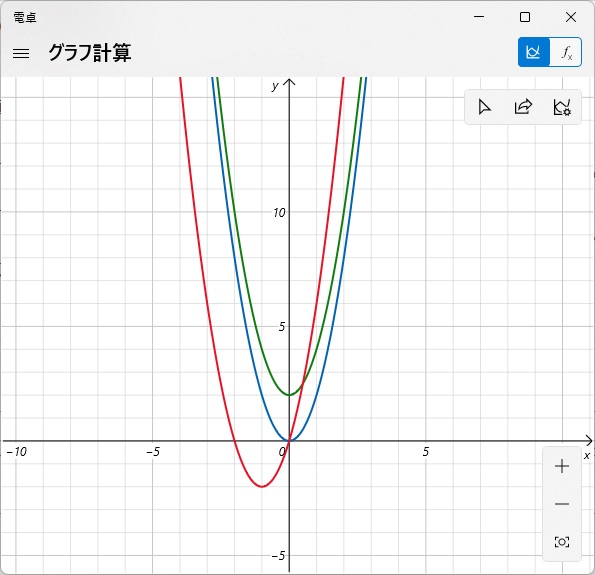
Windowsの電卓でグラフが書けるので、試してみましょう。(左上≡→グラフ計算)
頂点の位置は平方完成
二次関数で問題になるのが頂点に位置です。
ここが分かれば、その左右の点を少し計算するだけでグラフが書けます。
求め方ですが、平方完成しましょう。こちらは長くなるので別の記事にまとめてます。
あとがき
二次関数についてはこれぐらいのものです。
あと、通る点から二次関数を求める問題や、関数同士の交点の座標を求める問題がありますが、そちらは別のところでまとめようと思います。

説明が長くなるのと、使う基本知識が違うのじゃ。





コメント