【算数】かけ算のやり方は？

どうしてかけ算をするの？

どうしてかけ算を習うのでしょうか。

それは、計算が短時間でできるようになるからです。

例えば、3＋3＋3＋3＋3＝15 という式があります。これぐらいであれば、最初から順番に足していけば問題ないです。ただ、これより多くなってくると大変です。

3+3+3+3+3+3+3+3+3+3+3+3=36　これだと数えていかないとわかりません。

ただ、かけ算にすると式が短くなるだけでなく計算も簡単になります。

• 3+3+3+3+3+3+3+3+3+3+3+3=36
• 3×12=36

かけ算の順番はどちらでもよい

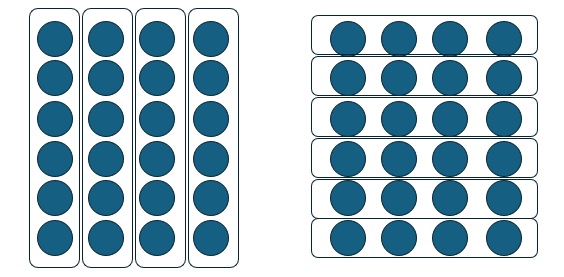
24という数は、上の図のようにグループ分けすることができます。

• 左：6が4つ
• 右：4が6つ

「6×4」や「4×6」とどちらで表してもいいです。

ただ、基本的には以下のように考えるようにしておくといいです。

• 左：6が4つ　6×4
• 右：4が6つ　4×6

九九を覚えよう

かけ算を毎回足し算で計算するのは大変です。

１×１から９×９までの結果を覚えてしまうことで、すぐに計算できるようにしましょう。

これを九九（くく）といいます。

×	1	2	3	4	5	6	7	8	9
1	1	2	3	4	5	6	7	8	9
2	2	4	6	8	10	12	14	16	18
3	3	6	9	12	15	18	21	24	27
4	4	8	12	16	20	24	28	32	36
5	5	10	15	20	25	30	35	40	45
6	6	12	18	24	30	36	42	48	54
7	7	14	21	28	35	42	49	56	63
8	8	16	24	32	40	48	56	64	72
9	9	18	27	36	45	54	63	72	81

あとがき

かけ算は、同じ数のたし算ということを知っていれば、中学高校になって文字が出てきても以下のように問題なく計算することができます。

• \(a\)が4つ　\(a+a+a+a=a×4=4a\)
• 4が\(a\)個　\(4×a＝4a\)

また、かけ算は面積だという考え方ができるようになるとさらにいろんな計算ができるようになるので頑張って覚えましょう。